LA VISIONE UV AVIARIA INCREMENTA I CONTRASTI DELLA SUPERFICIE FOGLIARE NELLE FORESTE
art. originale:
https://www.nature.com/articles/s41467-018-08142-5??utm_medium=affiliate&utm_source=commission_junction&utm_campaign=3_nsn6445_deeplink_PID7596328&utm_content=deeplink
Traduzione : Aurora R.
SOMMARIO
La visione UV è comune, tuttavia poco si conosce riguardo alla sua utilità in impieghi generali e comuni, come la risoluzione della struttura degli ambienti. Qui è possibile osservare ambienti con vegetazione usando una fotocamera multispettrale con canali che simulano la sensibilità fotorecettrice attraverso lo spettro UV visibile. Si può comprendere che il contrasto tra le superfici superiori e inferiori di una foglia è più alto in un canale UV rispetto a un qualsiasi canale visibile, e che questo fa sì che la posizione e l'orientamento della foglia risaltino chiaramente. Questa conclusione era alquanto inaspettata dal momento che entrambe le superfici della foglia riflettono similmente piccole proporzioni (1-2%) di luce UV incidente. Il forte contrasto UV può essere spiegato considerando che la luce di downwelling è più accesa di quella di upwelling, e che le foglie trasmettono < 0,06% di luce UV incidente. Le riflessioni speculari del cielo e della canopia soprastante dalla cuticola fogliare spesso fanno sembrare piccole delle riflessioni estese. Le riflessioni speculari cambiano il colore della foglia, tanto che il massimo contrasto fogliare è visibile a lunghezze d'onda UV brevi nelle canopie aperte, e ad ampie lunghezze d'onda nelle canopie chiuse.
INTRODUZIONE
Molti animali in grado di vedere i colori possiedono la capacità di vedere i raggi UV. Tuttavia l'intera gamma di mansioni a cui la visione UV potrebbe essere applicata rimane scarsamente esplorata a causa della difficoltà di fare previsioni su una gamma di lunghezza d'onda che non possiamo vedere. La maggior parte delle informazioni riguardanti l'utilità della visione UV è stata ricavata grazie a indagini mirate e specifiche per specie riguardo ai segnali inviati dai colori degli animali e dei fiori, e a deduzioni sul contrasto figura-sfondo che deve essere evidente per gli oggetti visti contro la luce del sole o in acque poco profonde. E' risaputo anche che il cielo è un potente emettitore di luce polarizzata e, che gli animali che usano schemi di polarizzazione basati sulla luce del cielo per lo spostamento, generalmente possiedono fotorecettori sensibili alla polarizzazione che raggiungono l'apice negli UV o nel blu. Al contrario, si sa poco dell'utilità della visione UV per visualizzare contrasti tra comuni oggetti terrestri incontrati dalla maggior parte degli animali che si trovano a terra nelle loro attività giornaliere. Un motivo per cui manca tale conoscenza è che è difficile prevedere quali confronti di oggetti possano generare alti contrasti UV, quando tutti gli oggetti in questione (ad es. foglie, tronchi, lettiera, rocce, ecc.) sono già noti per la riflessione della luce UV.
Per aggirare queste barriere e formulare ipotesi, si è fatto uso di una tecnologia sottoutilizzata nel campo dell'imaging visuale ecologico e multispettrale. Sono stati perfezionati canali di fotocamere, che imitavano la sensibilità spettrale degli animali, che hanno consentito di visualizzare i dati grezzi raccolti da fotorecettori. Questa tecnica ha compensato la nostra stessa incapacità di vedere gli UV e ha permesso di valutare quantitativamente il relativo beneficio di canali di fotorecettori differentemente sintonizzati attraverso lo specchio dell'UV visibile. Ha inoltre permesso di osservare ambienti quali si presentano, in situ, senza alterare la naturale geometria della luce.
E' stata adottata la visione tetracromatica aviaria come sistema di riferimento. La visione degli uccelli è un eccellente sistema di riferimento per numerose ragioni. Primo, gli uccelli che cercano cibo a terra impiegano molto del loro tempo a volare e/o a saltare attraverso la vegetazione, e molti cercano specifiche superfici fogliari per cacciare. Gli uccelli campionano l'intero spettro UV visibile, dall'UV al rosso, caratteristica che li rende un ottimo sistema per paragonare un canale UV all'intera gamma di canali visibili. In aggiunta, le sensibilità relative allo spettro del cono UV degli uccelli variano, particolare che ha reso possibile verificare se il tipo di ambiente possa condurre al perfezionamento delle sensibilità dello spettro UV negli uccelli e negli altri animali.
La visione UV è comune, tuttavia poco si conosce riguardo alla sua utilità in impieghi generali e comuni, come la risoluzione della struttura degli ambienti. Qui è possibile osservare ambienti con vegetazione usando una fotocamera multispettrale con canali che simulano la sensibilità fotorecettrice attraverso lo spettro UV visibile. Si può comprendere che il contrasto tra le superfici superiori e inferiori di una foglia è più alto in un canale UV rispetto a un qualsiasi canale visibile, e che questo fa sì che la posizione e l'orientamento della foglia risaltino chiaramente. Questa conclusione era alquanto inaspettata dal momento che entrambe le superfici della foglia riflettono similmente piccole proporzioni (1-2%) di luce UV incidente. Il forte contrasto UV può essere spiegato considerando che la luce di downwelling è più accesa di quella di upwelling, e che le foglie trasmettono < 0,06% di luce UV incidente. Le riflessioni speculari del cielo e della canopia soprastante dalla cuticola fogliare spesso fanno sembrare piccole delle riflessioni estese. Le riflessioni speculari cambiano il colore della foglia, tanto che il massimo contrasto fogliare è visibile a lunghezze d'onda UV brevi nelle canopie aperte, e ad ampie lunghezze d'onda nelle canopie chiuse.
INTRODUZIONE
Molti animali in grado di vedere i colori possiedono la capacità di vedere i raggi UV. Tuttavia l'intera gamma di mansioni a cui la visione UV potrebbe essere applicata rimane scarsamente esplorata a causa della difficoltà di fare previsioni su una gamma di lunghezza d'onda che non possiamo vedere. La maggior parte delle informazioni riguardanti l'utilità della visione UV è stata ricavata grazie a indagini mirate e specifiche per specie riguardo ai segnali inviati dai colori degli animali e dei fiori, e a deduzioni sul contrasto figura-sfondo che deve essere evidente per gli oggetti visti contro la luce del sole o in acque poco profonde. E' risaputo anche che il cielo è un potente emettitore di luce polarizzata e, che gli animali che usano schemi di polarizzazione basati sulla luce del cielo per lo spostamento, generalmente possiedono fotorecettori sensibili alla polarizzazione che raggiungono l'apice negli UV o nel blu. Al contrario, si sa poco dell'utilità della visione UV per visualizzare contrasti tra comuni oggetti terrestri incontrati dalla maggior parte degli animali che si trovano a terra nelle loro attività giornaliere. Un motivo per cui manca tale conoscenza è che è difficile prevedere quali confronti di oggetti possano generare alti contrasti UV, quando tutti gli oggetti in questione (ad es. foglie, tronchi, lettiera, rocce, ecc.) sono già noti per la riflessione della luce UV.
Per aggirare queste barriere e formulare ipotesi, si è fatto uso di una tecnologia sottoutilizzata nel campo dell'imaging visuale ecologico e multispettrale. Sono stati perfezionati canali di fotocamere, che imitavano la sensibilità spettrale degli animali, che hanno consentito di visualizzare i dati grezzi raccolti da fotorecettori. Questa tecnica ha compensato la nostra stessa incapacità di vedere gli UV e ha permesso di valutare quantitativamente il relativo beneficio di canali di fotorecettori differentemente sintonizzati attraverso lo specchio dell'UV visibile. Ha inoltre permesso di osservare ambienti quali si presentano, in situ, senza alterare la naturale geometria della luce.
E' stata adottata la visione tetracromatica aviaria come sistema di riferimento. La visione degli uccelli è un eccellente sistema di riferimento per numerose ragioni. Primo, gli uccelli che cercano cibo a terra impiegano molto del loro tempo a volare e/o a saltare attraverso la vegetazione, e molti cercano specifiche superfici fogliari per cacciare. Gli uccelli campionano l'intero spettro UV visibile, dall'UV al rosso, caratteristica che li rende un ottimo sistema per paragonare un canale UV all'intera gamma di canali visibili. In aggiunta, le sensibilità relative allo spettro del cono UV degli uccelli variano, particolare che ha reso possibile verificare se il tipo di ambiente possa condurre al perfezionamento delle sensibilità dello spettro UV negli uccelli e negli altri animali.
Si è compreso che l'ottica delle foglie e la geometria della luce dell'ambiente interagiscono per rendere la visione UV particolarmente adattabile a visualizzare i contrasti della superficie fogliare. Un canale UV dovrebbe perciò facilitare lo spostamento attraverso complessi ambienti ricchi di vegetazione, così come la localizzazione di particolari superfici fogliari per vari impieghi, inclusi la ricerca della preda, l'ovideposizione e la ricerca di rifugi. Usando il modellismo ottico, si può dimostrare che le riflessioni speculari nei differenti ambienti rivestono un ruolo sottovalutato nel creare l'apparente colore delle foglie e, in cambio, i contrasti della superficie fogliare. Per visualizzare i contrasti della superficie fogliare, le canopie chiuse favoriscono i fotorecettori di raggi UV a lunghezza d'onda maggiore. Questo risultato potrebbe avere delle implicazioni per la messa a punto di fotorecettori animali.
RISULTATI E DISCUSSIONE
E' stata utilizzata una fotocamera multispettrale di visione aviaria per visualizzare i contrasti attraverso il canale, paragonando due comuni varianti di coni UV (U e V, spesso indicati in letteratura con UVS e VS) a due comuni varianti di coni UV di S (blu) e M (verde) e di coni L (rosso) (Fig.1). Sono anche stati paragonati i due coni UV tra di loro. Ogni variante di cono UV è tipicamente accompagnata da una specifica variante di cono blu, così sono state confrontate anche le due varianti di cono blu tra di loro. Nello specifico, sono state cercate fonti di alto contrasto UV in ambienti ricchi di vegetazione che sono mancanti o più carenti in altri canali di colori, verificando come il contrasto UV contribuisca al contrasto di colore in sistemi visuali tetra, tri e dicromatici, e verificando se il tipo di ambiente influenzi la sintonia spettrale ottimale degli UV e delle sensibilità spettrali del fotorecettore blu.
Fig. 1
Le sensibilità spettrali dei coni aviari e dei canali della fotocamera multispettrale.
Le linee continue mostrano le sensibilità spettrali dei coni aviari e le linee tratteggiate mostrano i canali della fotocamera multispettrale. La maggior parte degli uccelli che cerca il cibo a terra è tetracromatica, con i coni L,M e sia S(U) sia U o S(V) e V. L,M, S, V e U indicano rispettivamente le lunghezze d'onda Lunga, Media, Corta, Violetta e Ultravioletta.
Le immagini sono stata divise in tre tipi di ambienti- (1) pascoli e porzioni della foresta dominati da vegetazione decidua nella Scania e in Svizzera, (2) foreste vergini di sclerofillo con un sottobosco di arbusti tipici della foresta pluviale ombreggiati da un'alta e aperta canopia di eucalipto nel Queensland, Australia, e (3) foreste pluviali tropicali e subtropicali vergini nel Queensland, Australia. Questi tre ambienti rappresentano una progressione dagli ambienti aperti e scarsamente ricoperti di vegetazione, agli ambienti chiusi e densamente ricoperti di vegetazione.
RISULTATI E DISCUSSIONE
E' stata utilizzata una fotocamera multispettrale di visione aviaria per visualizzare i contrasti attraverso il canale, paragonando due comuni varianti di coni UV (U e V, spesso indicati in letteratura con UVS e VS) a due comuni varianti di coni UV di S (blu) e M (verde) e di coni L (rosso) (Fig.1). Sono anche stati paragonati i due coni UV tra di loro. Ogni variante di cono UV è tipicamente accompagnata da una specifica variante di cono blu, così sono state confrontate anche le due varianti di cono blu tra di loro. Nello specifico, sono state cercate fonti di alto contrasto UV in ambienti ricchi di vegetazione che sono mancanti o più carenti in altri canali di colori, verificando come il contrasto UV contribuisca al contrasto di colore in sistemi visuali tetra, tri e dicromatici, e verificando se il tipo di ambiente influenzi la sintonia spettrale ottimale degli UV e delle sensibilità spettrali del fotorecettore blu.
Fig. 1
Le sensibilità spettrali dei coni aviari e dei canali della fotocamera multispettrale.
Le linee continue mostrano le sensibilità spettrali dei coni aviari e le linee tratteggiate mostrano i canali della fotocamera multispettrale. La maggior parte degli uccelli che cerca il cibo a terra è tetracromatica, con i coni L,M e sia S(U) sia U o S(V) e V. L,M, S, V e U indicano rispettivamente le lunghezze d'onda Lunga, Media, Corta, Violetta e Ultravioletta.
Le immagini sono stata divise in tre tipi di ambienti- (1) pascoli e porzioni della foresta dominati da vegetazione decidua nella Scania e in Svizzera, (2) foreste vergini di sclerofillo con un sottobosco di arbusti tipici della foresta pluviale ombreggiati da un'alta e aperta canopia di eucalipto nel Queensland, Australia, e (3) foreste pluviali tropicali e subtropicali vergini nel Queensland, Australia. Questi tre ambienti rappresentano una progressione dagli ambienti aperti e scarsamente ricoperti di vegetazione, agli ambienti chiusi e densamente ricoperti di vegetazione.
E' stata trovata un'evidente fonte di contrasto UV che mancava o era più carente nei canali dei coni visibili- il contrasto tra le superfici fogliari superiori e inferiori (d'ora in poi contrasto fogliare; calcolato come contrasto di Michelson). (Fig. 2,4,5 a, tabella 1).
Le superfici fogliari inferiori risultavano scure sotto gli UV, con le loro sagome che intensificavano la visibilità delle foglie e del perimetro delle foglie, e la geometria della struttura della vegetazione. Questo dettaglio strutturale, intensificato, potrebbe aumentare l'efficienza negli spostamenti in ambienti ricchi di vegetazione e nel localizzare particolari superfici fogliari per il nascondiglio, l'ovideposizione e la ricerca delle prede.
Fig.2
Esempi di immagini che mostrano la differenza nel contrasto fogliare visto da coni UV e verdi negli ambienti decidui nel sud della Svezia. Per ciascuna delle tre visuali, le due immagini in alto mostrano la stessa scena vista da canali fotorecettori UV e verdi. La variante di cono UV che ha visto il contrasto più alto è quella mostrata. Le due immagini in basso sono immagini RGB con colori falsati con tre dei quattro canali di coni aviari collegati ai canali R (rosso), G (verde) e B (blu) di uno schermo digitale. Per esempio, RGB=UMS denota che il cono U è mostrato dal canale rosso di uno schermo RGB, che il cono M da un canale verde, e il cono S da un canale blu. Si noti che la fila superiore di immagini RGB contiene un canale UV mentre quella inferiore no. Per fini di dimostrazione, i valori dei pixel dalle immagini originali sono stati (1) normalizzate dal valore di pixel medio in ogni immagine, (2) aggiustate per riempire la gamma dinamica di uno schermo digitale sRGB, e (3) aggiustate per disfare la portata di gamma sRGB della maggior parte degli schermi digitali. Ciò significa che, vista su uno schermo calibrato di sRGB, attraverso ciascun canale, l'intensità dei pixel ridimensiona linearmente l'output di un cono. Se un pixel è stato sovraesposto o sottoesposto in qualsiasi canale, il pixel corrispondente in tutti i canali è stato messo in bianco (per sovraesposto) o nero (per sottoesposto), ed escluso dai calcoli. Si noti che le immagini in colori falsati non possono replicare cosa gli animali vedano veramente, ma forniscono la migliore approssimazione a disposizione.
Fig. 3
Le superfici fogliari inferiori risultavano scure sotto gli UV, con le loro sagome che intensificavano la visibilità delle foglie e del perimetro delle foglie, e la geometria della struttura della vegetazione. Questo dettaglio strutturale, intensificato, potrebbe aumentare l'efficienza negli spostamenti in ambienti ricchi di vegetazione e nel localizzare particolari superfici fogliari per il nascondiglio, l'ovideposizione e la ricerca delle prede.
Fig.2
Esempi di immagini che mostrano la differenza nel contrasto fogliare visto da coni UV e verdi negli ambienti decidui nel sud della Svezia. Per ciascuna delle tre visuali, le due immagini in alto mostrano la stessa scena vista da canali fotorecettori UV e verdi. La variante di cono UV che ha visto il contrasto più alto è quella mostrata. Le due immagini in basso sono immagini RGB con colori falsati con tre dei quattro canali di coni aviari collegati ai canali R (rosso), G (verde) e B (blu) di uno schermo digitale. Per esempio, RGB=UMS denota che il cono U è mostrato dal canale rosso di uno schermo RGB, che il cono M da un canale verde, e il cono S da un canale blu. Si noti che la fila superiore di immagini RGB contiene un canale UV mentre quella inferiore no. Per fini di dimostrazione, i valori dei pixel dalle immagini originali sono stati (1) normalizzate dal valore di pixel medio in ogni immagine, (2) aggiustate per riempire la gamma dinamica di uno schermo digitale sRGB, e (3) aggiustate per disfare la portata di gamma sRGB della maggior parte degli schermi digitali. Ciò significa che, vista su uno schermo calibrato di sRGB, attraverso ciascun canale, l'intensità dei pixel ridimensiona linearmente l'output di un cono. Se un pixel è stato sovraesposto o sottoesposto in qualsiasi canale, il pixel corrispondente in tutti i canali è stato messo in bianco (per sovraesposto) o nero (per sottoesposto), ed escluso dai calcoli. Si noti che le immagini in colori falsati non possono replicare cosa gli animali vedano veramente, ma forniscono la migliore approssimazione a disposizione.
Fig. 3
Immagini esemplificative che mostrano la differenza nel contrasto fogliare visto dai coni UV e verdi negli ambienti umidi e sclerofilli nel Queensland, Australia. Vedi la Fig. 2 per maggiori dettagli.
Fig. 4
Immagini esemplificative che mostrano la differenza nel contrasto fogliare visto dai coni UV e verdi in ambienti di foresta pluviale nel Queensland, Australia. Vedi la Fig. 2 per maggiori dettagli.
Fig. 5
Il vantaggio della visione UV per visualizzare i contrasti fogliari acromatici e a colori. I grafici mostrano lo scarto interquartile mediano (IQR), e i dati più bassi e più alti, entro 1,5 IQR, sotto e sopra l'IQR (i valori anomali non sono mostrati). a I contrasti acromatici di Michelson visti da diversi canali di coni in ambienti differenti. In ogni ambiente, i coni UV hanno avuto un contrasto fogliare più alto che altri canali di coni a P<0,0001. b I contrasti a colori in unità di differenze appena avvertibili (JNDs) visti da un LMSU tetracromatico e tutte le combinazioni tricromatiche e dicromatiche possibili di fotorecettori aviari, ancora separati per ambiente. Per rendere i risultati il più generali possibile per il regno animale, si è supposto che tutte le composizioni di fotorecettori avessero lo stesso numero di ogni classe di fotorecettori in unità integrativa. In ogni ambiente, trasformare un tricromatico nella gamma visibile (LMS) in un tetracromatico con un cono UV (LMSU) ha reso evidente il contrasto di colori a P<0,0001. Tutte le composizioni del cono che contengono sia un cono U che M (evidenziate in arancione) hanno avuto un contrasto fogliare più alto di ogni altra composizione con lo stesso numero di coni a P<0,0001. Tutti i valori P derivano da test del segno a due lati, per esempio “signtest” in MATLAB. I dettagli dei test statistici possono essere trovati nella Tabella 1.
Fig. 4
Immagini esemplificative che mostrano la differenza nel contrasto fogliare visto dai coni UV e verdi in ambienti di foresta pluviale nel Queensland, Australia. Vedi la Fig. 2 per maggiori dettagli.
Fig. 5
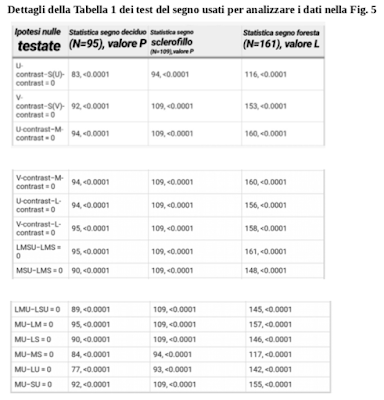
Il vantaggio della visione UV per visualizzare i contrasti fogliari acromatici e a colori. I grafici mostrano lo scarto interquartile mediano (IQR), e i dati più bassi e più alti, entro 1,5 IQR, sotto e sopra l'IQR (i valori anomali non sono mostrati). a I contrasti acromatici di Michelson visti da diversi canali di coni in ambienti differenti. In ogni ambiente, i coni UV hanno avuto un contrasto fogliare più alto che altri canali di coni a P<0,0001. b I contrasti a colori in unità di differenze appena avvertibili (JNDs) visti da un LMSU tetracromatico e tutte le combinazioni tricromatiche e dicromatiche possibili di fotorecettori aviari, ancora separati per ambiente. Per rendere i risultati il più generali possibile per il regno animale, si è supposto che tutte le composizioni di fotorecettori avessero lo stesso numero di ogni classe di fotorecettori in unità integrativa. In ogni ambiente, trasformare un tricromatico nella gamma visibile (LMS) in un tetracromatico con un cono UV (LMSU) ha reso evidente il contrasto di colori a P<0,0001. Tutte le composizioni del cono che contengono sia un cono U che M (evidenziate in arancione) hanno avuto un contrasto fogliare più alto di ogni altra composizione con lo stesso numero di coni a P<0,0001. Tutti i valori P derivano da test del segno a due lati, per esempio “signtest” in MATLAB. I dettagli dei test statistici possono essere trovati nella Tabella 1.
La statistica dei segni indica il numero di volte in cui la differenza nel contrasto fogliare visto da differenti canali o combinazioni di canali (mostrati nella colonna delle ipotesi nulle testate) era maggiore di zero.
Il canale verde è stato sorprendentemente inutile per visualizzare il contrasto fogliare (Fig. 2-4, 5 a, Tabella 1). Questo mette in dubbio l'intuizione che, poiché le foglie sono verdi, un canale verde dovrebbe essere il migliore per risolvere la struttura della vegetazione. L'impressionante differenza tra i canali verdi e UV può essere spiegata dal fatto che le foglie trasmettono e riflettono simili quantità di luce verde (e rossa e, in estensione minore, blu), ma riflettono molta più luce UV di quella che trasmettono. In natura, l'illuminazione downwelling è molto più chiara dell'illuminazione upwelling, che si traduce in più luce che è disponibile a riflettere dalle superfici superiori della foglia rispetto che da quelle inferiori. Questi fattori si combinano per fare sì che le superfici fogliari inferiori irradino simili quantità di verde, ma quantità di luce UV molto differenti.
In modo più specifico, nelle misurazioni della riflessione e trasmissione della superficie fogliare superiore in un intervallo di 300-500 nm (vedi Metodi), le foglie riflettono in maniera diffusa >25 volte la quantità di luce UV (300-400 nm) che trasmettono, ma riflettono soltanto 1,5 volte la quantità di luce blu (400-500 nm) che trasmettono. Indagini precedenti mostrano che le foglie riflettono e trasmettono simili quantità di luce verde (500-600 nm) e rossa (600-700), con la riflessione che varia la trasmissione da ~0,7 a 1,3 volte.
Il canale verde è stato sorprendentemente inutile per visualizzare il contrasto fogliare (Fig. 2-4, 5 a, Tabella 1). Questo mette in dubbio l'intuizione che, poiché le foglie sono verdi, un canale verde dovrebbe essere il migliore per risolvere la struttura della vegetazione. L'impressionante differenza tra i canali verdi e UV può essere spiegata dal fatto che le foglie trasmettono e riflettono simili quantità di luce verde (e rossa e, in estensione minore, blu), ma riflettono molta più luce UV di quella che trasmettono. In natura, l'illuminazione downwelling è molto più chiara dell'illuminazione upwelling, che si traduce in più luce che è disponibile a riflettere dalle superfici superiori della foglia rispetto che da quelle inferiori. Questi fattori si combinano per fare sì che le superfici fogliari inferiori irradino simili quantità di verde, ma quantità di luce UV molto differenti.
In modo più specifico, nelle misurazioni della riflessione e trasmissione della superficie fogliare superiore in un intervallo di 300-500 nm (vedi Metodi), le foglie riflettono in maniera diffusa >25 volte la quantità di luce UV (300-400 nm) che trasmettono, ma riflettono soltanto 1,5 volte la quantità di luce blu (400-500 nm) che trasmettono. Indagini precedenti mostrano che le foglie riflettono e trasmettono simili quantità di luce verde (500-600 nm) e rossa (600-700), con la riflessione che varia la trasmissione da ~0,7 a 1,3 volte.
Oltre a evidenziare il contrasto nel canale, è risaputo che in ogni ambiente, trasformare un tricromatico nell'intervallo visibile (LMS) aggiungendo un canale UV per renderlo un tetracromatico (LMSU) rende evidente il contrasto dei colori della foglia. (Fig. 5b, Tabella 1).
Ciò non sorprende, poiché aggiungere un canale colorato genera una nuova dimensione con la quale il colore può variare. Se si suppone nessun costo in termini di rumore aggiuntivo nei canali colorati preesistenti, un canale colorato aggiuntivo evidenzierà sempre il contrasto di colori se gli oggetti messi a confronto stimolano il nuovo canale anche solo con quantità leggermente differenti.
Ciò che risulta maggiormente interessante è che tutti i tricromatici e dicromatici teorici, che avevano sia fotorecettori UV che M, hanno visto un contrasto fogliare di colori più alto di qualsiasi altra composizione fotorecettrice che aveva lo stesso numero di canali fotorecettrici (Fig. 5b, Tabella 1).
La maggior parte dei vertebrati terrestri e degli invertebrati tricromatici e dicromatici hanno fotorecettori con picchi nelle stesse porzioni dello spettro dei coni aviari UV e M. Persino tra i mammiferi, si è recentemente scoperto che la sensibilità per gli UV è relativamente comune, con molte specie conosciute, o predette tali dalle sequenze di opsina, tali da avere picchi di coni UV, e con molte conosciute tali da avere lenti trasparenti alle lunghezze d'onda UV, che rendono possibile che anche i picchi dei coni blu (~400-450 nm) siano stimolati dalle lunghezze d'onda UV. Questa ricerca fornisce una ragione possibile per cui il contrasto UV è una sorgente di contrasto altamente campionata nel regno animale.
Sono stati inoltre eseguiti test sull'effetto del tipo di ambiente in una sintonia spettrale ottima dei coni UV e S. Il cono V era avvantaggiato a visualizzare i contrasti acromatici fogliari nella foresta pluviale e negli ambienti di sclerofillo e umidi, mentre il cono S(U) era avvantaggiato a visualizzare il contrasto acromatico fogliare in tutti gli ambienti (Fig. 6, Tabella 1). In tutti i tetracromatici LMSV, se si scambia il cono V con un cono U, o un cono S(V) con un cono S(U), uno alla volta, l'effetto nel contrasto di colori è molto simile all'effetto del contrasto acromatico nel canale. Tuttavia, poiché le varianti di coni U e S che si verificano non hanno gli stessi effetti direzionali nel contrasto nel canale, il loro effetto combinato nel contrasto di colori riflette un terreno intermedio tra i loro effetti individuali. Il risultato finale è che un sistema tetracromatico LMSU (con canali S(U) e U) era avvantaggiato a visualizzare contrasti di colori fogliari negli ambienti decidui e di sclerofillo e umidi.
Fig. 6
Ciò non sorprende, poiché aggiungere un canale colorato genera una nuova dimensione con la quale il colore può variare. Se si suppone nessun costo in termini di rumore aggiuntivo nei canali colorati preesistenti, un canale colorato aggiuntivo evidenzierà sempre il contrasto di colori se gli oggetti messi a confronto stimolano il nuovo canale anche solo con quantità leggermente differenti.
Ciò che risulta maggiormente interessante è che tutti i tricromatici e dicromatici teorici, che avevano sia fotorecettori UV che M, hanno visto un contrasto fogliare di colori più alto di qualsiasi altra composizione fotorecettrice che aveva lo stesso numero di canali fotorecettrici (Fig. 5b, Tabella 1).
La maggior parte dei vertebrati terrestri e degli invertebrati tricromatici e dicromatici hanno fotorecettori con picchi nelle stesse porzioni dello spettro dei coni aviari UV e M. Persino tra i mammiferi, si è recentemente scoperto che la sensibilità per gli UV è relativamente comune, con molte specie conosciute, o predette tali dalle sequenze di opsina, tali da avere picchi di coni UV, e con molte conosciute tali da avere lenti trasparenti alle lunghezze d'onda UV, che rendono possibile che anche i picchi dei coni blu (~400-450 nm) siano stimolati dalle lunghezze d'onda UV. Questa ricerca fornisce una ragione possibile per cui il contrasto UV è una sorgente di contrasto altamente campionata nel regno animale.
Sono stati inoltre eseguiti test sull'effetto del tipo di ambiente in una sintonia spettrale ottima dei coni UV e S. Il cono V era avvantaggiato a visualizzare i contrasti acromatici fogliari nella foresta pluviale e negli ambienti di sclerofillo e umidi, mentre il cono S(U) era avvantaggiato a visualizzare il contrasto acromatico fogliare in tutti gli ambienti (Fig. 6, Tabella 1). In tutti i tetracromatici LMSV, se si scambia il cono V con un cono U, o un cono S(V) con un cono S(U), uno alla volta, l'effetto nel contrasto di colori è molto simile all'effetto del contrasto acromatico nel canale. Tuttavia, poiché le varianti di coni U e S che si verificano non hanno gli stessi effetti direzionali nel contrasto nel canale, il loro effetto combinato nel contrasto di colori riflette un terreno intermedio tra i loro effetti individuali. Il risultato finale è che un sistema tetracromatico LMSU (con canali S(U) e U) era avvantaggiato a visualizzare contrasti di colori fogliari negli ambienti decidui e di sclerofillo e umidi.
Fig. 6
distribuzione per due varianti di coni S. I pannelli sulla destra mostrano gli stessi tipi di distribuzione per contrasti di colori visti da tetracromatici LMSV e LMSU. La linea nera verticale e spessa a x=0 indica il punto in cui le due varianti vedono un contrasto uguale. Il cono V è avvantaggiato a visualizzare i contrasti fogliari acromatici nella foresta pluviale (P<0,0001) e sclerofillo e umido (P=0,004), e il cono S(U) è avvantaggiato a visualizzare contrasti fogliari acromatici in tutti gli ambienti (P<0,0001). Un sistema tetracromatico LMSU è avvantaggiato a visualizzare il contrasto fogliare di colori negli ambienti decidui (P<0,0001) e di sclerofillo e umidi (P<0,0001). In questa figura sono state utilizzate le abbondanze relative di fotorecettori di uccelli che cercano il cibo a terra tali che il rapporto di coni L:M:S:U in un'unità integrativa è uguale a 3:2,5:1,7:1.
Il fatto che il cono S(U) veda quasi sempre un contrasto fogliare più alto del cono S(V), indipendentemente dall'ambiente, suggerisce che qualsiasi sintonia spettrale del cono S è probabilmente diretta da un'altra forza evolutiva estranea alla percezione del contrasto fogliare. D'altro canto, il fatto che le diverse varianti di cono UV vedano un contrasto fogliare massimo in diversi ambienti potrebbe spiegare, in parte, perché gli uccelli hanno ripetutamente fatto avanti e indietro tra due varianti di coni UV diversamente sintonizzate nella loro storia evolutiva, e potrebbe anche aiutare a spiegare la variazione nella sensibilità UV in altri gruppi di animali.
Per convalidare matematicamente l'effetto dell'ambiente e svelare la fisica dietro di esso è stato sviluppato un modello ottico per predire e paragonare i contrasti fogliari come visti dai coni V e U in diversi ambienti. Sono state misurate le proprietà spettrali delle foglie decidue e della foresta pluviale, e testati entrambi i tipi di foglie nel modello. Il modello è stato progettato per essere resistente al cambiamento dell'ambiente e programmato a ripetere i suoi calcoli 10000 volte, ogni volta randomizzando fino a 12 parametri di diversi ambienti (per la lista dei parametri, vedi Metodi: Calcoli del Modello Ottico). La distribuzione della differenza nel contrasto visto da coni V e U attraverso le 10000 ripetizioni del modello potrebbe poi essere rappresentata in un istogramma. Mettendo a confronto gli istogrammi generati dalle diverse combinazioni dei parametri, è stato possibile convalidare l'effetto dell'ambiente osservato nei dati multispettrali. Una volta convalidato, è stato rappresentato lo spettro generato durante i passaggi intermedi del modello per comprendere i meccanismi ottici dietro l'effetto. In ognuna delle piste dei modelli descritte sotto, si ritiene che tutti e 12 i parametri siano stati randomizzati, a meno che altrimenti specificati.
Quando il modello ottico includeva riflessioni profuse e trasmittanza soltanto, è stato impossibile mostrare qualsiasi condizione sotto la quale il cono V avrebbe visto un contrasto fogliare più alto del cono U (Fig. 7a, primo pannello). Per aumentare il realismo del modello, sono state introdotte riflessioni speculari di sorgenti luminose estese. Tali riflessioni infondono un colore uniforme sugli oggetti lisci e non dovrebbero essere confuse con i piccoli punti luminosi come quelli della luce solare direttamente riflessa (una sorgente puntiforme). L'identità della sorgente luminosa che è riflessa specularmente (d'ora in poi, sorgente luminosa speculare) potrebbe essere luce che si irradia dal cielo, dalle nuvole, dalla canopia o lettiera.
Fig. 7
Il fatto che il cono S(U) veda quasi sempre un contrasto fogliare più alto del cono S(V), indipendentemente dall'ambiente, suggerisce che qualsiasi sintonia spettrale del cono S è probabilmente diretta da un'altra forza evolutiva estranea alla percezione del contrasto fogliare. D'altro canto, il fatto che le diverse varianti di cono UV vedano un contrasto fogliare massimo in diversi ambienti potrebbe spiegare, in parte, perché gli uccelli hanno ripetutamente fatto avanti e indietro tra due varianti di coni UV diversamente sintonizzate nella loro storia evolutiva, e potrebbe anche aiutare a spiegare la variazione nella sensibilità UV in altri gruppi di animali.
Per convalidare matematicamente l'effetto dell'ambiente e svelare la fisica dietro di esso è stato sviluppato un modello ottico per predire e paragonare i contrasti fogliari come visti dai coni V e U in diversi ambienti. Sono state misurate le proprietà spettrali delle foglie decidue e della foresta pluviale, e testati entrambi i tipi di foglie nel modello. Il modello è stato progettato per essere resistente al cambiamento dell'ambiente e programmato a ripetere i suoi calcoli 10000 volte, ogni volta randomizzando fino a 12 parametri di diversi ambienti (per la lista dei parametri, vedi Metodi: Calcoli del Modello Ottico). La distribuzione della differenza nel contrasto visto da coni V e U attraverso le 10000 ripetizioni del modello potrebbe poi essere rappresentata in un istogramma. Mettendo a confronto gli istogrammi generati dalle diverse combinazioni dei parametri, è stato possibile convalidare l'effetto dell'ambiente osservato nei dati multispettrali. Una volta convalidato, è stato rappresentato lo spettro generato durante i passaggi intermedi del modello per comprendere i meccanismi ottici dietro l'effetto. In ognuna delle piste dei modelli descritte sotto, si ritiene che tutti e 12 i parametri siano stati randomizzati, a meno che altrimenti specificati.
Quando il modello ottico includeva riflessioni profuse e trasmittanza soltanto, è stato impossibile mostrare qualsiasi condizione sotto la quale il cono V avrebbe visto un contrasto fogliare più alto del cono U (Fig. 7a, primo pannello). Per aumentare il realismo del modello, sono state introdotte riflessioni speculari di sorgenti luminose estese. Tali riflessioni infondono un colore uniforme sugli oggetti lisci e non dovrebbero essere confuse con i piccoli punti luminosi come quelli della luce solare direttamente riflessa (una sorgente puntiforme). L'identità della sorgente luminosa che è riflessa specularmente (d'ora in poi, sorgente luminosa speculare) potrebbe essere luce che si irradia dal cielo, dalle nuvole, dalla canopia o lettiera.
Fig. 7
Il modello ottico convalida l'effetto dell'ambiente osservato nei dati mutispettrali e rivela il meccanismo dietro di esso. a Primo Pannello: quando solo la riflessione diffusa e trasmittanza erano modellate, il cono U ha sempre visto un contrasto fogliare più alto, indipendentemente dal fatto che venissero usati spettri di foglie decidue o della foresta pluviale. Secondo pannello: quando le riflessioni speculari erano aggiunte al modello, il cono V a volte ha visto un contrasto fogliare più alto, ma non c'era alcuna separazione netta tra i tipi di foglie decidue e della foresta pluviale. Terzo pannello: illustrando le foglie illuminate da diverse sorgenti luminose speculari si è scoperto che il cono V ha visto un contrasto fogliare più alto solo quando le foglie sovrastanti erano la sorgente luminosa speculare. Quarto pannello: mettendo a confronto gli ambienti con diverse quantità di canopia sovrastante, è stata dimostrata una netta separazione tra ambienti aperti e chiusi, con il cono V che vedeva un contrasto fogliare più alto in ambienti chiusi (<80% copertura di canopia) e con il cono U che vedeva un contrasto fogliare più alto in ambienti aperti (<80& copertura di canopia). Si deduce che le differenze viste tra gli ambienti erano dovute alle differenze nell'apertura degli ambienti e non dalle proprietà ottiche delle foglie. b Gli spettri di radianza mediana delle superfici fogliari modellate con e senza riflessioni speculari quando la sorgente luminosa speculare erano le foglie sovrastanti. Il tipo di foglia (deciduo o della foresta pluviale) era randomizzato. Qui, si può notare che le riflessioni speculari dalla superficie superiore della foglia cambiano la forma spettrale della riflettanza della superficie fogliare superiore più che della riflettanza della superficie fogliare inferiore, e che questa differenza è più pronunciata in ambienti chiusi. Il risultato di ciò in termini di contrasto acromatico mediano attraverso lo spettro blu UV può essere visto nei due pannelli in basso. In ambienti chiusi (pannello in basso a destra), la riflessione speculare cambia la luminosità della superficie fogliare superiore tanto che il contrasto diventa più alto ad alte lunghezze d'onda. Si noti che tutti i parametri degli ambienti che non vengono menzionati nella figura sono stati randomizzati in ogni 10000 ripetizioni del modello.
Dopo aver aggiunto riflessioni speculari da entrambe le superfici superiori e inferiori delle foglie, il modello ottico ha mostrato che il cono V a volte ha visto un contrasto fogliare più alto del cono U (Fig. 7 a, secondo pannello). Tuttavia, non è stata notata nessuna differenza nella tendenza centrale dei contrasti fogliari modellati con le foglie decidue e della foresta pluviale. Confrontando il contrasto fogliare per le foglie illuminate da diverse sorgenti luminose speculari, si è notato che il cono V ha visto un contrasto fogliare più alto dell cono U solo quando la sorgente luminosa speculare giungeva da foglie sovrastanti. (Fig. 7 a, terzo pannello). Poiché gli ambienti di foresta pluviale campionati erano molto più densi di quelli decidui, si suppone che la differenza nella sintonia spettrale ottimale tra gli ambienti potrebbe derivare dalle differenze nella probabilità delle foglie sovrastanti di essere la sorgente luminosa speculare. Perciò è stato testato un effetto di copertura di canopia nel modello ottico. Quando la canopia era >80% chiusa, era più probabile che il cono V vedesse contrasti fogliari più alti che il cono U (Fig 7 a, quarto pannello). Al contrario, quando la canopia era <80% chiusa, era più probabile che il cono U vedesse un contrasto fogliare più alto del cono V. Questo suggerisce che la copertura di canopia giochi un ruolo fondamentale nelle differenze nella sintonia spettrale ottimale osservata negli ambienti.
Per comprendere meglio come le riflessioni speculari possano cambiare la sensibilità spettrale ottimale nel cono V, sono state disegnate le radianze mediane delle foglie modellate con e senza le riflessioni speculari quando la sorgente luminosa speculare erano le foglie sovrastanti. (Fig. 7 b). Quando la copertura di canopia era >80% (Fig. 7 b, pannello destro in alto), la sorgente luminosa speculare cambiava la forma spettrale della radianza della superficie superiore della foglia molto di più di quando la copertura di canopia era <80% (Fig. 7b, pannello sinistro in alto). Questo non era vero per le superfici fogliari inferiori -le riflessioni speculari hanno cambiato soprattutto l'intensità e non la forma spettrale della radianza della superficie inferiore della foglia, e funzionava così in proporzioni simili sotto tutti i livelli di copertura di canopia. In breve, le riflessioni speculari hanno cambiato la forma spettrale della radianza diversamente per le superfici fogliari superiori e inferiori, e questo cambiamento è più estremo negli ambienti chiusi. Il risultato in termini di contrasto
Dopo aver aggiunto riflessioni speculari da entrambe le superfici superiori e inferiori delle foglie, il modello ottico ha mostrato che il cono V a volte ha visto un contrasto fogliare più alto del cono U (Fig. 7 a, secondo pannello). Tuttavia, non è stata notata nessuna differenza nella tendenza centrale dei contrasti fogliari modellati con le foglie decidue e della foresta pluviale. Confrontando il contrasto fogliare per le foglie illuminate da diverse sorgenti luminose speculari, si è notato che il cono V ha visto un contrasto fogliare più alto dell cono U solo quando la sorgente luminosa speculare giungeva da foglie sovrastanti. (Fig. 7 a, terzo pannello). Poiché gli ambienti di foresta pluviale campionati erano molto più densi di quelli decidui, si suppone che la differenza nella sintonia spettrale ottimale tra gli ambienti potrebbe derivare dalle differenze nella probabilità delle foglie sovrastanti di essere la sorgente luminosa speculare. Perciò è stato testato un effetto di copertura di canopia nel modello ottico. Quando la canopia era >80% chiusa, era più probabile che il cono V vedesse contrasti fogliari più alti che il cono U (Fig 7 a, quarto pannello). Al contrario, quando la canopia era <80% chiusa, era più probabile che il cono U vedesse un contrasto fogliare più alto del cono V. Questo suggerisce che la copertura di canopia giochi un ruolo fondamentale nelle differenze nella sintonia spettrale ottimale osservata negli ambienti.
Per comprendere meglio come le riflessioni speculari possano cambiare la sensibilità spettrale ottimale nel cono V, sono state disegnate le radianze mediane delle foglie modellate con e senza le riflessioni speculari quando la sorgente luminosa speculare erano le foglie sovrastanti. (Fig. 7 b). Quando la copertura di canopia era >80% (Fig. 7 b, pannello destro in alto), la sorgente luminosa speculare cambiava la forma spettrale della radianza della superficie superiore della foglia molto di più di quando la copertura di canopia era <80% (Fig. 7b, pannello sinistro in alto). Questo non era vero per le superfici fogliari inferiori -le riflessioni speculari hanno cambiato soprattutto l'intensità e non la forma spettrale della radianza della superficie inferiore della foglia, e funzionava così in proporzioni simili sotto tutti i livelli di copertura di canopia. In breve, le riflessioni speculari hanno cambiato la forma spettrale della radianza diversamente per le superfici fogliari superiori e inferiori, e questo cambiamento è più estremo negli ambienti chiusi. Il risultato in termini di contrasto
fogliare da 300 a 500 nm può essere visto nei due pannelli in basso nella Fig. 7b. Quando la copertura di canopia era >80%, il contrasto fogliare era superiore a 400 nm, mentre quando la copertura di canopia era <80%, il contrasto fogliare era inferiore a 400 nm.
Si può supporre che la ragione per cui le riflessioni speculari cambiano la radianza fogliare più negli ambienti chiusi che aperti sia che negli ambienti chiusi le riflessioni speculari hanno un'intensità maggiore rispetto alle riflessioni diffuse. In un ambiente chiuso, passa poca luce attraverso i buchi nella canopia per contribuire alle riflessioni diffuse. Come tale, il rapporto di riflessioni speculari a riflessioni diffuse sarà più alto in un ambiente chiuso, spiegando perché le riflessioni speculari cambiano la radianza fogliare più in ambienti chiusi che aperti. Per capire meglio questa relazione, è stato usato il modello per visualizzare l'interrelazione tra la copertura di canopia, l'intensità di riflessioni speculari a riflessioni diffuse, e il contrasto fogliare visto da il cono V rispetto al cono U. Come previsto, quando la copertura di canopia aumentava, la proporzione di riflesione speculare a riflessioni diffuse aumentava, e allo stesso modo anche il contrasto fogliare visto dal cono V rispetto al cono U (Fig. 8).
Fig. 8
Si può supporre che la ragione per cui le riflessioni speculari cambiano la radianza fogliare più negli ambienti chiusi che aperti sia che negli ambienti chiusi le riflessioni speculari hanno un'intensità maggiore rispetto alle riflessioni diffuse. In un ambiente chiuso, passa poca luce attraverso i buchi nella canopia per contribuire alle riflessioni diffuse. Come tale, il rapporto di riflessioni speculari a riflessioni diffuse sarà più alto in un ambiente chiuso, spiegando perché le riflessioni speculari cambiano la radianza fogliare più in ambienti chiusi che aperti. Per capire meglio questa relazione, è stato usato il modello per visualizzare l'interrelazione tra la copertura di canopia, l'intensità di riflessioni speculari a riflessioni diffuse, e il contrasto fogliare visto da il cono V rispetto al cono U. Come previsto, quando la copertura di canopia aumentava, la proporzione di riflesione speculare a riflessioni diffuse aumentava, e allo stesso modo anche il contrasto fogliare visto dal cono V rispetto al cono U (Fig. 8).
Fig. 8
Il rapporto di riflessioni speculari a riflessioni diffuse dalle foglie modifica la sintonia spettrale ottimale per percepire il contrasto fogliare. Il modello ottico rivela che la sensibilità spettrale ottimale per visualizzare il contrasto fogliare dipende non solo dalla sorgente luminosa speculare (vedi Fig. 7 a) ma anche dal rapporto di riflessioni speculari a riflessioni diffuse dalla superficie fogliare superiore. Il rapporto dipende da quanto il cielo è oscurato dalla canopia sovrastante. Meno luce passa attraverso i buchi della canopia sovrastante, più grande è la proporzione di riflessioni speculari rispetto a riflessioni diffuse, e più vantaggioso il cono V per visualizzare il contrasto fogliare. La linea y=0 indica il punto in cui entrambe le varianti del cono V vedono un contrasto uguale.
Studi precedenti hanno testato quali parti dello spettro un animale dovrebbe campionare per la discriminazione di colori ottimale in ambienti ricchi di vegetazione. Tuttavia, limitazioni metodologiche hanno impedito di scoprire l'importanza dell'UV. Lythgoe e Partridge (1989) hanno portato delle foglie in laboratorio per misurare la loro riflettanza spettrale e hanno mostrato, con modelli, che un fotorecettore blu e verde è la migliore combinazione dicromatica per discriminare tra le diverse foglie verdi. Non è chiaro se abbiano messo a confronto le superfici superiori e inferiori delle foglie, ma portando oggetti in laboratorio hanno demolito gli effetti della geometria dell'illuminazione, che è cruciale per impostare un forte contrasto fogliare UV. Chiao et al. ha usato una fotocamera multispettrale per testare quali combinazioni dicromatiche di fotorecettori vedano i contrasti di colori più alti in ambienti ricchi di vegetazione, ma non campionato lo spettro UV. Questo studio è il primo a usare un sistema di imaging spettrale multi o iper per visualizzare la vegetazione, in situ, dalla prospettiva di un animale attraverso l'intero spettro UV visibile. Poichè la metodologia utilizzata ha preservato la naturale geometria dell'illuminazione e ha campionato l'intero spettro UV visibile, è stato possibile scoprire un fenomeno che, in esame retrospettivo,
Studi precedenti hanno testato quali parti dello spettro un animale dovrebbe campionare per la discriminazione di colori ottimale in ambienti ricchi di vegetazione. Tuttavia, limitazioni metodologiche hanno impedito di scoprire l'importanza dell'UV. Lythgoe e Partridge (1989) hanno portato delle foglie in laboratorio per misurare la loro riflettanza spettrale e hanno mostrato, con modelli, che un fotorecettore blu e verde è la migliore combinazione dicromatica per discriminare tra le diverse foglie verdi. Non è chiaro se abbiano messo a confronto le superfici superiori e inferiori delle foglie, ma portando oggetti in laboratorio hanno demolito gli effetti della geometria dell'illuminazione, che è cruciale per impostare un forte contrasto fogliare UV. Chiao et al. ha usato una fotocamera multispettrale per testare quali combinazioni dicromatiche di fotorecettori vedano i contrasti di colori più alti in ambienti ricchi di vegetazione, ma non campionato lo spettro UV. Questo studio è il primo a usare un sistema di imaging spettrale multi o iper per visualizzare la vegetazione, in situ, dalla prospettiva di un animale attraverso l'intero spettro UV visibile. Poichè la metodologia utilizzata ha preservato la naturale geometria dell'illuminazione e ha campionato l'intero spettro UV visibile, è stato possibile scoprire un fenomeno che, in esame retrospettivo,
sembra ovvio, ma che nessuno studio precedente ha avuto la capacità metodologica o la lungimiranza di cercare.
Sviluppando un modello ottico per capire la fisica dietro ai dati multispettrali, si è scoperto che le riflessioni speculari hanno un ruolo sottovalutato nel cambiare la forma spettrale della luce riflessa da oggetti lisci. Studi di colorazione adattabile generalmente non spiegano le riflessioni speculari. Questo potrebbe aver portato a risultati ingannevoli in alcuni casi, soprattutto quando si guarda a parti dello spettro dove le riflessioni speculari spesso sovrastano quelle diffuse. Il presente studio perciò apre la possibilità di un intero nuovo mondo di indagine sull'importanza delle riflessioni speculari per l'evoluzione della visione e colori negli ambienti naturali.
METODI
Design del filtro della fotocamera multispettrale
Per calcolare lo spettro del filtro target sono state calcolate le tipiche sensibilità spettrali dei coni aviari e poi divisi questi spettri per le sensibilità/trasmittanze degli altri componenti del sistema della fotocamera, che era basato sullo Spectrocam PIXELTEQ's UV-VIS (Largo, FL, USA). Usando i dati tabulati in Hart e Vorobyev, è stata calcolata la bassa lunghezza d'onda del picco della sensibilità per l'opsina in ogni classe di cono aviario (U,V,S,M,L) e usate queste lunghezze d'onda per generare curve di sensibilità spettrale di opsina seguendo Govardoviskii et al. Poi, è stata calcolata la bassa lunghezza d'onda del picco del coefficiente di assorbimento al 50%(λmid) di ogni classe di gocciolina d'olio, inclusa una media separata per ciascuna delle due varianti che può essere accoppiata con la classe di cono S(blu). Per ogni media λmid, è stato calcolato il corrispondente λcut e poi la trasmittanza spettrale di ogni gocciolina d'olio, usando equazioni modello sviluppate da Hart e Vorobyev. Lo spettro di trasmittanza della media ottica degli uccelli con ciascuna variante della classe del cono UV (U e V) è stato calcolato dai dati tabulati in Lind et al.
E' stata calcolata la sensibilità spettrale desiderata di ogni canale di fotocamera multispettrale moltiplicando ogni curva di opsina con la sua gocciolina d'olio associata per lo spettro di trasmittanza della media oculare. Per i coni M e L, è stata utilizzata la media dello spettro di trasmittanza ottica U e V. Per ottenere lo spettro di trasmittanza del filtro target, sono state divise queste sensibilità spettrali del target per lo spettro di efficienza quantistica del sensore della fotocamera (JAI CM-140 GE-UV, Kushima City, Giappone), per lo spettro di trasmitttanza delle lenti (Jenoptik CoastalOpt UV-VIS-IR 60 mm 1:4 Apo Macro, Jupiter, FL, USA), e per un filtro di blocco infrarosso montato davanti alle lenti (commissionato da Knight Optical, Kent, UK). Perciò,
Sviluppando un modello ottico per capire la fisica dietro ai dati multispettrali, si è scoperto che le riflessioni speculari hanno un ruolo sottovalutato nel cambiare la forma spettrale della luce riflessa da oggetti lisci. Studi di colorazione adattabile generalmente non spiegano le riflessioni speculari. Questo potrebbe aver portato a risultati ingannevoli in alcuni casi, soprattutto quando si guarda a parti dello spettro dove le riflessioni speculari spesso sovrastano quelle diffuse. Il presente studio perciò apre la possibilità di un intero nuovo mondo di indagine sull'importanza delle riflessioni speculari per l'evoluzione della visione e colori negli ambienti naturali.
METODI
Design del filtro della fotocamera multispettrale
Per calcolare lo spettro del filtro target sono state calcolate le tipiche sensibilità spettrali dei coni aviari e poi divisi questi spettri per le sensibilità/trasmittanze degli altri componenti del sistema della fotocamera, che era basato sullo Spectrocam PIXELTEQ's UV-VIS (Largo, FL, USA). Usando i dati tabulati in Hart e Vorobyev, è stata calcolata la bassa lunghezza d'onda del picco della sensibilità per l'opsina in ogni classe di cono aviario (U,V,S,M,L) e usate queste lunghezze d'onda per generare curve di sensibilità spettrale di opsina seguendo Govardoviskii et al. Poi, è stata calcolata la bassa lunghezza d'onda del picco del coefficiente di assorbimento al 50%(λmid) di ogni classe di gocciolina d'olio, inclusa una media separata per ciascuna delle due varianti che può essere accoppiata con la classe di cono S(blu). Per ogni media λmid, è stato calcolato il corrispondente λcut e poi la trasmittanza spettrale di ogni gocciolina d'olio, usando equazioni modello sviluppate da Hart e Vorobyev. Lo spettro di trasmittanza della media ottica degli uccelli con ciascuna variante della classe del cono UV (U e V) è stato calcolato dai dati tabulati in Lind et al.
E' stata calcolata la sensibilità spettrale desiderata di ogni canale di fotocamera multispettrale moltiplicando ogni curva di opsina con la sua gocciolina d'olio associata per lo spettro di trasmittanza della media oculare. Per i coni M e L, è stata utilizzata la media dello spettro di trasmittanza ottica U e V. Per ottenere lo spettro di trasmittanza del filtro target, sono state divise queste sensibilità spettrali del target per lo spettro di efficienza quantistica del sensore della fotocamera (JAI CM-140 GE-UV, Kushima City, Giappone), per lo spettro di trasmitttanza delle lenti (Jenoptik CoastalOpt UV-VIS-IR 60 mm 1:4 Apo Macro, Jupiter, FL, USA), e per un filtro di blocco infrarosso montato davanti alle lenti (commissionato da Knight Optical, Kent, UK). Perciò,
dove
Si(λ) = sensibilità spettrale della classe di coni i,
Ti(λ) = trasmittanza spettrale delle goccioline d'olio associate con la classe di coni i,
Tm,i(λ) = trasmittanza spettrale di media ottica (lenti, cornea, liquido vitreo) associato con la classe
Si(λ) = sensibilità spettrale della classe di coni i,
Ti(λ) = trasmittanza spettrale delle goccioline d'olio associate con la classe di coni i,
Tm,i(λ) = trasmittanza spettrale di media ottica (lenti, cornea, liquido vitreo) associato con la classe
di coni i,
Ftarget,i(λ) = trasmittanza spettrale target del filtro di fotocamera multispettrale, Ssensor(λ) = sensibilità spettrale del sensore della fotocamera,
Tlens(λ) = trasmittanza spettrale delle lenti della fotocamera, e
TIRblock(λ) = trasmittanza spettrale del filtro di blocco infrarosso.
PIXELTEQ (Largo, FL, USA) ha fabbricato i filtri secondo il Ftarger,i(λ) calcolato. Un confronto tra le sensibilità di spettro aviario e le sensibilità spettrali effettive di ciascun canale di fotocamera è raffigurato nella Fig. 1.
Campionamento e fotografia dell'ambiente
Sono state acquisite 173 serie di sei fotografie (una attraverso ciascuno dei sei filtri) di ambienti terrestri ricchi di vegetazione, inclusi gli ambienti decidui nel sud della Svezia (43 serie) e degli ambienti di sclerofillo e umidi (50 serie) e foreste pluviali (80 serie) nel Queensland, Australia. I dettagli dei siti possono essere trovati nella Tabella Supplementare 1. Le fotografie sono state scattate nei vari siti in giorni sereni o in porzioni del giorno per minimizzare la confusione dovuta al movimento dei rami e delle foglie indotto dal vento. Le escursioni sul campo sono state pianificate per massimizzare la gamma di condizioni di illuminazione campionate, da cieli nuvolosi a sgombri, e dall'alba al crepuscolo. Per ogni scena campionata, la posizione e la direzione della fotocamera è stata selezionata in una maniera pseudo-casuale disegnata per massimizzare la gamma di condizioni dell'ambiente e dell'illuminazione campionata, incluso, quando possibile, le differenti altezze nella canopia, con il sussidio delle cosiddette canopy tower, dei sentieri, dei ponti, ecc. Le fotografie degli ambienti decidui sono limitate al mese di giugno, luglio e agosto per evitare gli effetti della senescenza fogliare che avrebbero potuto creare confusione. Quando la gamma dinamica della fotocamera era insufficiente ad acquisire gran parte della gamma dinamica della scena, sono state scattate serie multiple di fotografie e in seguito assemblate nel MATLAB per creare immagini con gamma altamente dinamica.
Quantificare il contrasto fogliare dalle fotografie
Il risultato finale del sensore della fotocamera dello Spetrocam UV-VIS saliva in modo lineare con l'intensità luminosa; perciò, non sono state richieste correzioni non lineari. Il rumore termico era costante attraverso le esposizioni ed è stato sottratto da tutti i valori dei pixel. Ogni valore del pixel di una fotografia scattata con un filtro dato rappresentava il quantum catch per una singola classe di coni in un singolo punto nello spazio. Per adattare i quantum catch all'intensità dello sfondo, ogni valore del pixel è stato normalizzato con la media di tutti i valori dei pixel nella fotografia. Ogni serie di sei fotografie è poi stato aperta usando il software Evince (Prediktera, Umea, Svezia). Con questo programma, sono state selezionate a mano tutte le superfici superiori delle foglie e tutte quelle inferiori, selezionando gli stessi pixel attraverso le sei fotografie. Ogni specie di pianta è stata selezionata separatamente. Sono stati esportati gli indici dei pixel selezionati e poi importati nel MATLAB, che è stato usato per calcolare il quantum catch mediano della superficie superiore delle foglie di ogni pianta e poi della superficie inferiore in ogni fotografia. Questi mediani sono stati poi usati per calcolare il contrasto di Michelson e le differenze appena avvertibili (JNDs) tra le superfici fogliari superiori e inferiori di ogni pianta. Le JNDs sono state calcolate con una trasformazione logaritmica dei quantum catch. Per il nostro paragone tra uccelli LMSU e LMSV, le frazioni di Weber sono state calcolate da stime di rapporti segnale-rumore e frazioni di coni di uccelli che cercano il cibo a terra. Le frazioni di Weber usate sono le seguenti: U e V: 0,12, S: 0,092, M: 0,075,
Ftarget,i(λ) = trasmittanza spettrale target del filtro di fotocamera multispettrale, Ssensor(λ) = sensibilità spettrale del sensore della fotocamera,
Tlens(λ) = trasmittanza spettrale delle lenti della fotocamera, e
TIRblock(λ) = trasmittanza spettrale del filtro di blocco infrarosso.
PIXELTEQ (Largo, FL, USA) ha fabbricato i filtri secondo il Ftarger,i(λ) calcolato. Un confronto tra le sensibilità di spettro aviario e le sensibilità spettrali effettive di ciascun canale di fotocamera è raffigurato nella Fig. 1.
Campionamento e fotografia dell'ambiente
Sono state acquisite 173 serie di sei fotografie (una attraverso ciascuno dei sei filtri) di ambienti terrestri ricchi di vegetazione, inclusi gli ambienti decidui nel sud della Svezia (43 serie) e degli ambienti di sclerofillo e umidi (50 serie) e foreste pluviali (80 serie) nel Queensland, Australia. I dettagli dei siti possono essere trovati nella Tabella Supplementare 1. Le fotografie sono state scattate nei vari siti in giorni sereni o in porzioni del giorno per minimizzare la confusione dovuta al movimento dei rami e delle foglie indotto dal vento. Le escursioni sul campo sono state pianificate per massimizzare la gamma di condizioni di illuminazione campionate, da cieli nuvolosi a sgombri, e dall'alba al crepuscolo. Per ogni scena campionata, la posizione e la direzione della fotocamera è stata selezionata in una maniera pseudo-casuale disegnata per massimizzare la gamma di condizioni dell'ambiente e dell'illuminazione campionata, incluso, quando possibile, le differenti altezze nella canopia, con il sussidio delle cosiddette canopy tower, dei sentieri, dei ponti, ecc. Le fotografie degli ambienti decidui sono limitate al mese di giugno, luglio e agosto per evitare gli effetti della senescenza fogliare che avrebbero potuto creare confusione. Quando la gamma dinamica della fotocamera era insufficiente ad acquisire gran parte della gamma dinamica della scena, sono state scattate serie multiple di fotografie e in seguito assemblate nel MATLAB per creare immagini con gamma altamente dinamica.
Quantificare il contrasto fogliare dalle fotografie
Il risultato finale del sensore della fotocamera dello Spetrocam UV-VIS saliva in modo lineare con l'intensità luminosa; perciò, non sono state richieste correzioni non lineari. Il rumore termico era costante attraverso le esposizioni ed è stato sottratto da tutti i valori dei pixel. Ogni valore del pixel di una fotografia scattata con un filtro dato rappresentava il quantum catch per una singola classe di coni in un singolo punto nello spazio. Per adattare i quantum catch all'intensità dello sfondo, ogni valore del pixel è stato normalizzato con la media di tutti i valori dei pixel nella fotografia. Ogni serie di sei fotografie è poi stato aperta usando il software Evince (Prediktera, Umea, Svezia). Con questo programma, sono state selezionate a mano tutte le superfici superiori delle foglie e tutte quelle inferiori, selezionando gli stessi pixel attraverso le sei fotografie. Ogni specie di pianta è stata selezionata separatamente. Sono stati esportati gli indici dei pixel selezionati e poi importati nel MATLAB, che è stato usato per calcolare il quantum catch mediano della superficie superiore delle foglie di ogni pianta e poi della superficie inferiore in ogni fotografia. Questi mediani sono stati poi usati per calcolare il contrasto di Michelson e le differenze appena avvertibili (JNDs) tra le superfici fogliari superiori e inferiori di ogni pianta. Le JNDs sono state calcolate con una trasformazione logaritmica dei quantum catch. Per il nostro paragone tra uccelli LMSU e LMSV, le frazioni di Weber sono state calcolate da stime di rapporti segnale-rumore e frazioni di coni di uccelli che cercano il cibo a terra. Le frazioni di Weber usate sono le seguenti: U e V: 0,12, S: 0,092, M: 0,075,
L: 0,069. Per il confronto tra tetracromatici e tricromatici teorici, e dicromatici (Fig. 5b), si è voluta massimizzare la generalità dei risultati nel regno animale, così è stato presupposto che lo stesso numero di ogni classe di fotorecettori abbia contribuito a un'unità integrativa, e impostato tutte le frazioni di Weber a 0,069.
Se alcune foglie in un'immagine erano illuminate dalla luce del sole diretta, queste foglie sono state selezionate e analizzate separatamente. Se c'erano pixel sovra o sottoesposti in un canale, questi pixel sono stati esclusi da tutti i calcoli in tutti i canali. I valori di pixel selezionati e normalizzati e i loro metadati associati possono essere scaricati come un file JSON nel sito https://figshare.com/ sotto il DOI 10.6084/m9.figshare.7423532.
Parametri dei risultati del modello ottico
Per determinare le riflettanze diffuse dello spettro e le trasmittanze delle foglie sono state misurate queste proprietà da 17 foglie decidue raccolte dal campus dell'Università Lund, e da 16 foglie di foresta pluviale raccolte dalla serra del Giardino Botanico dell'Università Lund a metà giugno. Le specie decidue campionate sono : Acer platanoides, Alnus incana, Betula pubescens, Cornus sanguinea, Corylus avellana, Crataegus laevigata, Crataegus monogyna, Fagus sylvatica, Fallopia dumetorum, Malus spp., Prunus padus, Quercus rubra, Rhamnus cathartica, Rosa spp., Sorbus aucuparia, and Taraxacum pallidipes. Le specie della foresta pluviale campionate sono: Aglaonema nitidum, Anchomanes difformis, Arpophyllum giganteum, Artocarpus altilis, Bambusa vulgaris, Camillia japonica, Corynocarpus laevigatus, Encephalartus ferox, Epipremnum pinnatum, Myriocarpa spp., Passiflora quadrangularis, Psidium cattleianum, Syngonium podophyllum, and Theobromum cacao.
Per determinare un tipico spettro di riflettanza di lettiera sono state misurate le riflettanze spettrali diffuse delle superfici di 17 foglie secche trovate nel lettiera del campus e dei parchi a Lund, Svezia. Le foglie morte non sono state identificate nelle specie, ma l'ispezione visiva ha indicato che provenivano tutte da specie differenti.
La riflettanza diffusa è stata misurata con una sonda di riflessione, orientata a 45° dalla superficie della foglia, connessa a uno spettroscopio USB2000 + UV-VIS-ES e una sorgente luminosa DH- 2000 (entrambe dall'Ocean Optics, Dunedin, FL, USA). La trasmittanza è stata misurata con una Sfera di Ulbricht (Electro Optical Industries Inc., Santa Barbara, CA, USA) connessa a uno spettrometro USB2000 + UV-VIS-ES, con il cielo sgombro come sorgente luminosa. Per ogni classe di spettri, è stato calcolato lo spettro mediano da usare come modello di risultato (Figura Supplementare 1 a).
Sono stati utilizzati gli spettri di irradianza terrestre standard dell'American Society for Testing and Materials' (ASTM) come modello ottico. Questi includono l'irradianza diretta normale solare Is per un sole a 42° dallo zenit, e l'irradianza semisferica Ia per luce incidente su una superficie inclinata a 37° verso lo stesso sole sotto cieli sgombri. L'irradianza semisferica di cieli sgombri Ib è stata calcolata sottraendo Is da Ia. L'irradianza di cieli nuvolosi è stata calcolata da Ib e Is seguendo la parametrizzazione di Siegel et al. usando il cloud index (indice nuvola) CL di 0,8 che è tipico di condizioni nuvolose per calcolare il cloud index spettrale cl,
Se alcune foglie in un'immagine erano illuminate dalla luce del sole diretta, queste foglie sono state selezionate e analizzate separatamente. Se c'erano pixel sovra o sottoesposti in un canale, questi pixel sono stati esclusi da tutti i calcoli in tutti i canali. I valori di pixel selezionati e normalizzati e i loro metadati associati possono essere scaricati come un file JSON nel sito https://figshare.com/ sotto il DOI 10.6084/m9.figshare.7423532.
Parametri dei risultati del modello ottico
Per determinare le riflettanze diffuse dello spettro e le trasmittanze delle foglie sono state misurate queste proprietà da 17 foglie decidue raccolte dal campus dell'Università Lund, e da 16 foglie di foresta pluviale raccolte dalla serra del Giardino Botanico dell'Università Lund a metà giugno. Le specie decidue campionate sono : Acer platanoides, Alnus incana, Betula pubescens, Cornus sanguinea, Corylus avellana, Crataegus laevigata, Crataegus monogyna, Fagus sylvatica, Fallopia dumetorum, Malus spp., Prunus padus, Quercus rubra, Rhamnus cathartica, Rosa spp., Sorbus aucuparia, and Taraxacum pallidipes. Le specie della foresta pluviale campionate sono: Aglaonema nitidum, Anchomanes difformis, Arpophyllum giganteum, Artocarpus altilis, Bambusa vulgaris, Camillia japonica, Corynocarpus laevigatus, Encephalartus ferox, Epipremnum pinnatum, Myriocarpa spp., Passiflora quadrangularis, Psidium cattleianum, Syngonium podophyllum, and Theobromum cacao.
Per determinare un tipico spettro di riflettanza di lettiera sono state misurate le riflettanze spettrali diffuse delle superfici di 17 foglie secche trovate nel lettiera del campus e dei parchi a Lund, Svezia. Le foglie morte non sono state identificate nelle specie, ma l'ispezione visiva ha indicato che provenivano tutte da specie differenti.
La riflettanza diffusa è stata misurata con una sonda di riflessione, orientata a 45° dalla superficie della foglia, connessa a uno spettroscopio USB2000 + UV-VIS-ES e una sorgente luminosa DH- 2000 (entrambe dall'Ocean Optics, Dunedin, FL, USA). La trasmittanza è stata misurata con una Sfera di Ulbricht (Electro Optical Industries Inc., Santa Barbara, CA, USA) connessa a uno spettrometro USB2000 + UV-VIS-ES, con il cielo sgombro come sorgente luminosa. Per ogni classe di spettri, è stato calcolato lo spettro mediano da usare come modello di risultato (Figura Supplementare 1 a).
Sono stati utilizzati gli spettri di irradianza terrestre standard dell'American Society for Testing and Materials' (ASTM) come modello ottico. Questi includono l'irradianza diretta normale solare Is per un sole a 42° dallo zenit, e l'irradianza semisferica Ia per luce incidente su una superficie inclinata a 37° verso lo stesso sole sotto cieli sgombri. L'irradianza semisferica di cieli sgombri Ib è stata calcolata sottraendo Is da Ia. L'irradianza di cieli nuvolosi è stata calcolata da Ib e Is seguendo la parametrizzazione di Siegel et al. usando il cloud index (indice nuvola) CL di 0,8 che è tipico di condizioni nuvolose per calcolare il cloud index spettrale cl,
Per ottenere l'irradianza semisferica per un cielo nuvoloso Ic, il cloud index spettrale è stato moltiplicato per l'irradianza semisferica sotto un cielo sgombro. L'irradianza semisferica sotto un cielo sgombro Ics è stata prima calcolata aggiungendo l'irradianza di cielo sgombro Ib all'irradianza solare Is ponderata dal coseno dell'angolo θz dello zenit solare,
Gli spettri di irradianza semisferica del cielo, delle nuvole e del cielo sotto un angolo solare di zero sono mostrati nella Figura Supplementare 1b. Le radianze di cielo e nuvola steradiante sono state stimate dividendo le loro radianze per pi. Sebbene l'intensità della radianza di nuvola e di cielo può variare in base alla posizione del sole e alla densità e spessore della nuvola, le intensità radianti del cielo con condizioni variabili e della nuvola non hanno effetti rilevanti nell'output del nostro modello ottico (per es. la differenza nel contrasto fogliare visto dalle due varianti di coni aviari UV).
Gli spettri di irradianza semisferica del cielo, delle nuvole e del cielo sotto un angolo solare di zero sono mostrati nella Figura Supplementare 1b. Le radianze di cielo e nuvola steradiante sono state stimate dividendo le loro radianze per pi. Sebbene l'intensità della radianza di nuvola e di cielo può variare in base alla posizione del sole e alla densità e spessore della nuvola, le intensità radianti del cielo con condizioni variabili e della nuvola non hanno effetti rilevanti nell'output del nostro modello ottico (per es. la differenza nel contrasto fogliare visto dalle due varianti di coni aviari UV).
Calcoli del modello ottico
Il modello ottico è stato programmato per ripetere i calcoli del contrasto fogliare del cono U e V 10000 volte con 12 parametri che, a meno che altrimenti dichiarati, sono stati randomizzati ogni volta per spiegare la variazione naturale nella geometria dell'ambiente e nelle condizioni ambientali. I parametri randomizzati includono (1) l'angolo dello zenit solare, (2) l'inclinazione verticale delle foglie di cui veniva calcolato il contrasto, (3) l'azimut del sole rispetto alla direzione dello sguardo dello spettatore, (4) la copertura di nuvole, (5) se le foglie di cui veniva calcolato il contrasto erano al sole o all'ombra, (6) la proporzione del sole occluso dalla canopia sovrastante, (7) l'occlusione del sole per le nuvole, (8) la proporzione del terreno (es. lettiera) visibile attraverso la vegetazione sottostante, (9) l'identità della sorgente luminosa speculare riflessa dalla superficie fogliare superiore (poteva essere luce che si irradiava dal cielo, dalle nuvole o dalla canopia sovrastante), (10) l'identità della sorgente luminosa speculare riflessa dalla superficie inferiore della foglia (poteva essere luce che si irradiava dalla canopia sottostante o dalla lettiera), (11) se la sorgente luminosa speculare nel (10) era illuminata dalla luce diretta del sole, e (12) se venivano usati spettri di foglie decidue o della foresta pluviale. Quando ciascuno di questi parametri è definito nelle equazioni che seguono, il suo numero corrispondente in questa lista è mostrato tra parentesi.
Per semplicità, si presume che lo sguardo dell'osservatore aviario sia orizzontale, es. perpendicolare alla direzione dello zenit (Figura Supplementare 1c). Il modello ha calcolato il contrasto acromatico tra le superfici superiori e inferiori di due foglie identiche, fianco a fianco, una con la superficie superiore inclinata verso l'osservatore, e l'altra con la superficie superiore non inclinata verso l'osservatore. L'angolo di inclinazione θ1 delle due foglie rispetto allo zenit era lo stesso entro un'iterazione data e poteva spaziare tra 70 e 90°. Per semplicità, si presume che tutte le altre superfici di riflessione nella foresta (altre foglie nella canopia e lettiera) siano orientate orizzontalmente.
Quando nessun oggetto sovrastante (canopia, nuvole) bloccava la luce del sole diretta, il modello ha calcolato gli angoli di incidenza θs del sole sopra la superficie superiore di ciascuna delle due foglie. Per fare ciò, si è seguito:
Per semplicità, si presume che lo sguardo dell'osservatore aviario sia orizzontale, es. perpendicolare alla direzione dello zenit (Figura Supplementare 1c). Il modello ha calcolato il contrasto acromatico tra le superfici superiori e inferiori di due foglie identiche, fianco a fianco, una con la superficie superiore inclinata verso l'osservatore, e l'altra con la superficie superiore non inclinata verso l'osservatore. L'angolo di inclinazione θ1 delle due foglie rispetto allo zenit era lo stesso entro un'iterazione data e poteva spaziare tra 70 e 90°. Per semplicità, si presume che tutte le altre superfici di riflessione nella foresta (altre foglie nella canopia e lettiera) siano orientate orizzontalmente.
Quando nessun oggetto sovrastante (canopia, nuvole) bloccava la luce del sole diretta, il modello ha calcolato gli angoli di incidenza θs del sole sopra la superficie superiore di ciascuna delle due foglie. Per fare ciò, si è seguito:
(9)
dove
θz = angolo dello zenit solare (parametro #1)
θ1 = angolo inclinato della foglia rispetto allo zenit (parametro #2) e,
quando la superficie superiore della foglia era inclinata verso l'osservatore,
γs = azimut del sole rispetto alla direzione dello sguardo dello spettatore (parametro #3) e, quando la superficie superiore della foglia non era inclinata verso lo spettatore,
γs = γs – 180°.
Se θs era ≥ 90°, l'angolo del sole rispetto alla foglia era tale che il sole non colpiva la foglia. Quando ciò avveniva, l'immediatezza dell'illuminazione del sole sulla foglia d (definita e implementata sotto) era impostata a zero.
L'incidente di irradianza spettrale di downwelling sopra la superficie superiore della foglia inclinata verso l'osservatore è stato poi approssimato dagli spettri ottenuti nella sezione precedente, calcolando i contributi relativi della luce solare diretta, luce delle nuvole, luce del sole, luce che filtra attraverso le foglie:
e poi sommando questi contributi per ottenere l'incidente di irradianza spettrale di downwelling totale sulla foglia:
θz = angolo dello zenit solare (parametro #1)
θ1 = angolo inclinato della foglia rispetto allo zenit (parametro #2) e,
quando la superficie superiore della foglia era inclinata verso l'osservatore,
γs = azimut del sole rispetto alla direzione dello sguardo dello spettatore (parametro #3) e, quando la superficie superiore della foglia non era inclinata verso lo spettatore,
γs = γs – 180°.
Se θs era ≥ 90°, l'angolo del sole rispetto alla foglia era tale che il sole non colpiva la foglia. Quando ciò avveniva, l'immediatezza dell'illuminazione del sole sulla foglia d (definita e implementata sotto) era impostata a zero.
L'incidente di irradianza spettrale di downwelling sopra la superficie superiore della foglia inclinata verso l'osservatore è stato poi approssimato dagli spettri ottenuti nella sezione precedente, calcolando i contributi relativi della luce solare diretta, luce delle nuvole, luce del sole, luce che filtra attraverso le foglie:
e poi sommando questi contributi per ottenere l'incidente di irradianza spettrale di downwelling totale sulla foglia:
dove
pc = proporzione del cielo occluso dalle nuvole (parametro #4),
Ib = irradianza downwelling del cielo blu,
Ic = irradianza downwelling del cielo nuvoloso,
d = indica se la luce del sole diretta è bloccata dalle foglie sovrastanti (0 = sì, 1 = no) (parametro #5)
Is = irradianza solare con elevazione di 90°
T = trasmittanza delle foglie,
p1 = proporzione del cielo occluso dalle foglie sovrastanti (parametro #6), e
ps = occlusione del sole per le nuvole (0 = occlusione totale, 1 = nessuna occlusione) (parametro #7)
La radianza per steradiante dovuta alla riflettanza diffusa dalla superficie superiore delle foglie è stata calcolata come:
pc = proporzione del cielo occluso dalle nuvole (parametro #4),
Ib = irradianza downwelling del cielo blu,
Ic = irradianza downwelling del cielo nuvoloso,
d = indica se la luce del sole diretta è bloccata dalle foglie sovrastanti (0 = sì, 1 = no) (parametro #5)
Is = irradianza solare con elevazione di 90°
T = trasmittanza delle foglie,
p1 = proporzione del cielo occluso dalle foglie sovrastanti (parametro #6), e
ps = occlusione del sole per le nuvole (0 = occlusione totale, 1 = nessuna occlusione) (parametro #7)
La radianza per steradiante dovuta alla riflettanza diffusa dalla superficie superiore delle foglie è stata calcolata come:
Si noti che il componente lsun del ldown deve essere calcolato separatamente per la riflettanza diffusa della superficie superiore della foglia e trasmittanza della superficie inferiore della foglia, in quanto l'angolo del sole incidente sulla foglia sarebbe diverso nei due casi.
La radianza per steradiante dovuta alla riflettanza diffusa dalla superficie inferiore della foglia è stata determinata calcolando prima l'irradianza upwelling come prodotto dell'irradianza downwelling e della riflettanza degli oggetti (foglie e lettiera) sotto la foglia:
dove
pg = proporzione del terreno visibile attraverso la vegetazione sottostante (parametro #8), e
Rg = riflettanza della lettiera.
Questa irradianza upwelling è stata poi usata per calcolare la riflettanza diffusa della superficie inferiore della foglia:
La radianza per steradiante dovuta alla riflettanza diffusa dalla superficie inferiore della foglia è stata determinata calcolando prima l'irradianza upwelling come prodotto dell'irradianza downwelling e della riflettanza degli oggetti (foglie e lettiera) sotto la foglia:
dove
pg = proporzione del terreno visibile attraverso la vegetazione sottostante (parametro #8), e
Rg = riflettanza della lettiera.
Questa irradianza upwelling è stata poi usata per calcolare la riflettanza diffusa della superficie inferiore della foglia:
Rl = riflettanza della superficie inferiore della foglia.
Per calcolare la radianza spettrale proveniente dalle foglie dovuta alle riflessioni speculari, sono state seguite le equazioni di Fresnel. È stato usato un fattore di correzione conservativa K di 1 per le superfici superiori e inferiori; Brakke (1994) ha scoperto che la foglia K può spaziare da 0,6 a 3,5, e che a volte la superficie superiore ha una K maggiore della superficie inferiore, e a volte viceversa. Le conclusioni tratte dal modello sono state le stesse indipendentemente da dove la K è stata impostata per le superfici superiori e inferiori entro la gamma 0,6-3,5. I componenti polarizzati orizzontalmente Rs e verticalmente Rp della riflettanza sono stati calcolati come:
Per calcolare la radianza spettrale proveniente dalle foglie dovuta alle riflessioni speculari, sono state seguite le equazioni di Fresnel. È stato usato un fattore di correzione conservativa K di 1 per le superfici superiori e inferiori; Brakke (1994) ha scoperto che la foglia K può spaziare da 0,6 a 3,5, e che a volte la superficie superiore ha una K maggiore della superficie inferiore, e a volte viceversa. Le conclusioni tratte dal modello sono state le stesse indipendentemente da dove la K è stata impostata per le superfici superiori e inferiori entro la gamma 0,6-3,5. I componenti polarizzati orizzontalmente Rs e verticalmente Rp della riflettanza sono stati calcolati come:
L'indice refrattivo dell'aria, n1, è stato impostato a 1. L'indice refrattivo delle foglie, n2, è stato impostato a 1,45. L'indice refrattivo delle foglie è stato approssimato come costante con una lunghezza d'onda in quanto non ci sono misurazioni pubblicate o modelli sotto a 400 nm. n2 potrebbe aumentare in modo evidente vicino a 300 nm a causa dell'assorbimento della cuticola della foglia; tuttavia, impostare l'indice refrattivo per aumentare linearmente da 1,45 al valore più alto registrato in un materiale naturale (4,14 a 1800 nm nel Germanio) da 350 a 300 nm, o da 400 a 300 nm, non ha avuto effetti rilevanti nell'output del modello. Nell'iterazione di ogni modello, le sorgenti luminose speculari sopra e sotto (parametri #9 e #10) erano sorgenti luminose estese che sono state scelte casualmente con una probabilità definita dalle proporzioni relative dei diversi oggetti nell'ambiente. Se, per esempio, come sorgente luminosa speculare da sopra fossero state selezionate casualmente le foglie sovrastanti, allora la radianza della sorgente luminosa speculare per steradiante sarebbe stata calcolata come:
e la radianza per steradiante di luce che riflette specularmente la superficie superiore della foglia sarebbe stata calcolata come:
e la radianza per steradiante di luce che riflette specularmente la superficie superiore della foglia sarebbe stata calcolata come:
La sorgente di luce speculare da sotto (es. luce diffusamente riflessa dalle foglie o dalla lettiera) è stata casualmente selezionata in un modello simile. La radianza di questa sorgente luminosa è stata calcolata con l'immediatezza della luce solare (dr) sulla superficie riflessiva di upwelling come parametro randomizzato (0 o 1) (parametro #11), secondo la proporzione del cielo occluso dalle nuvole o dalle foglie. Se, per esempio, la lettiera fosse stata selezionata come sorgente di luce speculare, allora la radianza di questa sorgente luminosa speculare per steradiante sarebbe stata calcolata come:
Si = sensibilità spettrale della classe di coni i,
Tm,i = spettro di trasmittanza della media ottica (cornea, lenti, vitreo) associata con la classe di coni i.
Questi due ultimi parametri sono gli stessi di quelli usati per progettare i filtri su misura per lo Spectrocam (vedi “Modello del filtro della fotocamera” sopra). Si noti che i coni U e V hanno goccioline d'olio trasparenti, così lo spettro di trasmittanza della goccia d'olio qui è stata omessa. Il contrasto acromatico di Michelson tra le superfici fogliari superiori e inferiori è stato calcolato
come:
Tm,i = spettro di trasmittanza della media ottica (cornea, lenti, vitreo) associata con la classe di coni i.
Questi due ultimi parametri sono gli stessi di quelli usati per progettare i filtri su misura per lo Spectrocam (vedi “Modello del filtro della fotocamera” sopra). Si noti che i coni U e V hanno goccioline d'olio trasparenti, così lo spettro di trasmittanza della goccia d'olio qui è stata omessa. Il contrasto acromatico di Michelson tra le superfici fogliari superiori e inferiori è stato calcolato
come:
R>0 indica che il cono V vedrebbe un contrasto fogliare più alto, R<0 indica che il cono U vedrebbe un contrasto fogliare più alto, e R=0 indica che i cono V e U vedrebbero un contrasto fogliare uguale.
Disponibilità del codice
Il codice MATLAB usato per eseguire le analisi è disponibile dall'autore corrispondente sotto richiesta.
Sommario
Maggiori informazioni sul modello dell'esperimento è disponibile nel Naure Research Reporting Summary collegato a questo articolo.
Disponibilità dei dati
La sorgente dei dati sotto le Fig. 5-6 e delle Tabelle 1-2 possono essere trovate al sito https://figshare.com/ sotto il DOI 10.6084/m9.figshare.7423532. Un sommario per questo Articolo è disponibile come Summplementary Information File.
Disponibilità del codice
Il codice MATLAB usato per eseguire le analisi è disponibile dall'autore corrispondente sotto richiesta.
Sommario
Maggiori informazioni sul modello dell'esperimento è disponibile nel Naure Research Reporting Summary collegato a questo articolo.
Disponibilità dei dati
La sorgente dei dati sotto le Fig. 5-6 e delle Tabelle 1-2 possono essere trovate al sito https://figshare.com/ sotto il DOI 10.6084/m9.figshare.7423532. Un sommario per questo Articolo è disponibile come Summplementary Information File.